SVM学习记录
最近又看了一些关于支持向量机的知识，记录一下自己的学习心得，总的来说SVM还是非常好的分类器算法，能够找到一个关于问题的最优解，但是面临一个很大的问题就是很多时候可能会无法找到合适的核函数去解决问题，其实整个SVM的学习个人推荐b站一个up主的讲解视频（av28186618），讲解整个算法从Hard-Margin到核函数再到Soft-Margin都很清楚，但是还是缺少我比较想学习的SMO算法，但是其实这个算法的实现对于SVM来说不是太重要的核心知识，李航老师和周志华老师的书中都介绍得比较浅，机器学习实战中有代码可以去看看。它是一个解决规划问题的解法而已，所以个人认为不完全理解原理也是可以的。
Hard-Margin
首先SVM是一个判别模型，区别于贝叶斯的生成模型，其实区分两个模型最直接的方法就是，判别模型是估计概率P(x|y)，而生成模型是估计P(x,y)的概率，然后Margin的意思就是离超平面最近的点和超平面之间的距离，SVM的目的就是使整个Margin变大，因为最大的Margin可以使分类的情况变大最好。下图解释了什么似margin，我们的目的就是令这个margin最大：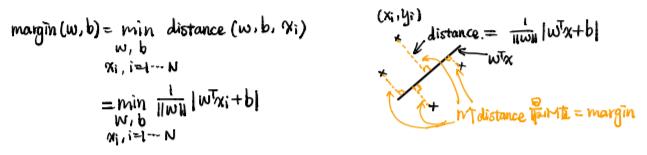 
其实我们的w的不同，点与直线的距离也会随之等距离扩大的。道理就是4x1 = 2x2 +4 和2x1 =x2 +2 所表达的直线是一样的，但是一个点和他们的距离根据距离公式运算出来的大小是不一样的。所以我们就可以将这个最小的距离做一个规定，令他等于1。这个做法可以方便后面的运算。这样我们就可以得到关于这个问题的一个规划限制和目标值。如下图所示： 
之后我们就可以利用拉格朗日乘子法构造一个与之对应的对偶问题。首先我们利用乘子构造如下一个式子，拉格朗日乘子法的目的就是利用最大化这个函数而去除掉我们的大于0约束，将约束转化成λ的约束。 
然后我们的目标还是要求整个margin的最小值，因此问题经过变化后就变成了最小最大问题，根据强对偶条件，可以转换成最大最小问题。然后我们可以对w和b进行求导，求导之后我们就可以将w和b用参数去表示。整个问题就变成了下面的形式：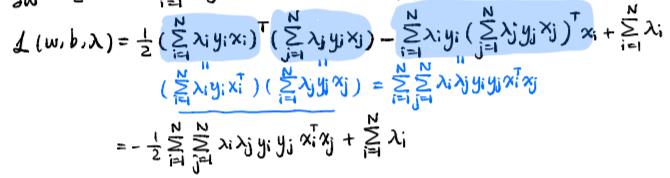 
其实上述描述的过程就是KKT条件生成的过程，一个原问题转化成拉格朗日问题的前提就是必须满足KKT条件，如下图：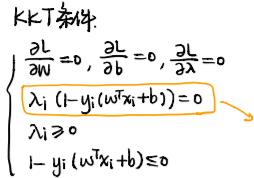 
Soft-Margin
在数据手机过程中往往会有错误标识的脏数据或者叫做干扰，所以我们的模型应该容许这个错误的存在。因此就有了Soft的方法建模。一种记录错误的方法是将越过超平的边界的数据点进行记录，但是这种方法得到的函数并不可导，另一种方法是记录超越超平面的边界的数据点和边界的距离，这个函数是连续的。因此问题的规划变成下面的形式，当然我们再最小化的时候不能让这个错误起到很大的作用，因此我们要对错误的计数添加一个约束参数C来进行限制。当C取较大值时候代表我们的允许出错的程度较低，反之，程度会运行出错程度要大一些。然后再利用拉格朗日乘子法构造对偶问题，过程基本类似，但是多了一个参数η，就不再赘述了。
Kernel-Function
出现核函数的原因是，很多问题我们在低维空间无法解决，因此我们必须对问题进行升高维度，最简单的例子就是异或问题。而升高唯的方法其实很简单，例如我们可以把x1变成x1+x12。因此存在一个变换函数使得x1变成x1+x12。但是回到我们要解决的问题，我们可以发现求解的规划问题中都是两个样本进行内积相乘，在实际的应用中，我们往往很大找到上面的变换函数，但是我们如果可以找到两个样本变换后内积相乘的函数也能达到一样的效果。因此我们曲线救国，不去寻找这样的变换函数，而直接去寻找我们的变换后的内积函数，而这个变换后的内积函数就是我们的核函数。找到核函数后，我们的做法就和上面的两种情况类似，同样是根据KKT条件和拉格朗日乘子法去进行问题转换。常见的核函数有线性核（Linear Kernel），多项式核（Polynomial Kernel），径向基核函数（Radial Basis Function）或者叫高斯核函数。 