论文研读-小数据集处理方法
暑假期间读了几篇关于小数据集处理的论文，都是针对一些数据集数量不够而进行机器学习的情况，主要是来自一篇Survey的总结，然后根据Survey的思路去进行的学习总结，今天有空写一下研读的体会，以便日后忘记
概括
这篇Survey的标题是Learning from Small Data Set to Build Classification Model:A Survey，虽然发会议不是什么大会，但是里面所提及到的论文还是很有参考价值的。这篇Survey首先介绍了一些常用的分类的学习方法，决策树啊，贝叶斯啊一堆。然后入正题，介绍了几种针对用小数据集进行机器学习的处理方法。其中个人觉得比较有意思的是：A diffusion-neural-network for learning from small samples中提到的方法，其余几个方法也是根据它进行的改进，另一个就是：Using mega-trend-diffusion and artificial samples in small data set learning for early flexible manufacturing system scheduling knowledge。
这篇论文花了很大段篇幅去介绍概念，可能这是一篇2004年的论文，人们对于机器学习还不是十分了解。经过了许多介绍之后，论文来到了第四章，也是我觉得比较精彩的一个篇章。论文中用到的是x和y这对兄弟，目的就是用x去模拟出一些u，从而使数据集变得更加多，方便接下来的训练。文中用x作为一个实际存在的样本，然后利用的关键估计工具是高斯分布。文中将要估计的u假设成一个符合x为均值的随机变量，那样就可以在x的附近随机模拟出几个近似但可能不等于x的假设数u。这就是全文的关键思路。除了均值之外，高斯分还需要有方差，方差使用的是作者推荐的一个计算公式，如下图所示：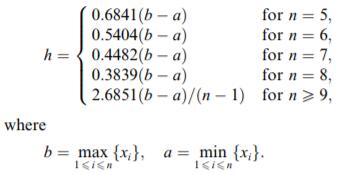 
既然有了高斯分布去模拟x，那么一定要有一个范围，并不是所有的符合这个高斯分布的u都可以成为假设的x。这是作者用了一个阈值，这个阈值衡量的是高斯分布的概率密度函数的取值，我们知道这个函数是一个山的形状，可以理解为波峰附近的变量和均值相似。所以只要设定一个阈值，概率密度大于这个阈值的变量u的取值才能使用。而作者提出的关于这个阈值的设定使用的是x和y（这里是真实样本）的相关系数，也就是Pearson相关系数，系数等0证明x和y无关，系数接近1或-1证明x和y相关性强。作者巧妙地利用x和y的相关系数去束缚x的假设取值u也是十分巧妙。但是作者后提出这个取值会使计算最后不收敛，所以他取用了精度更高的方法（就是说x和u更加接近），加入x和y的相关系数r=0.9，那么阈值就取0.999999，6个9。这样就得到了估计的x，同时y也用同样的方法估计得到作为估计x的标签。
随后人们慢慢地发现上的方法存在一定的问题，其中最明显的问题无疑就是机器学习中的大难题：过拟合。因为经过这样的方法估计出来的x和y都是在原样本附近的点，导致这些数据很集中，导致模型会尽量地往这些点靠拢，使得模型的泛化性能变差。然后很快就有人提出了改进版本：Using mega-trend-diffusion and artificial samples in small data set learning for early flexible manufacturing system scheduling knowledge。这篇文章在原方法上加多了一个mega，这个方法主要是针对分类问题，文中假设有一系列的x属于A类别，一系列x属于B，他的目的就是去通过这些x去模拟出一下其他的数据，增加这个x的维度，使得这些维度成为x的一些支撑，当然他们依旧是A类别的，简单地说就是把一个本是ax1+b=y的函数变成ax1+a1x11+a2x12+…+anx1n+b=y，后面这些x就是估计样本数据。具体的方法如下所示：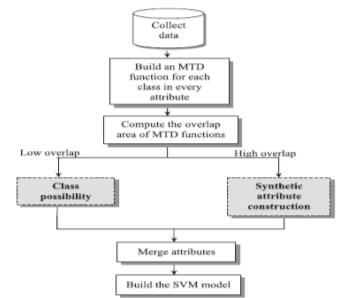 
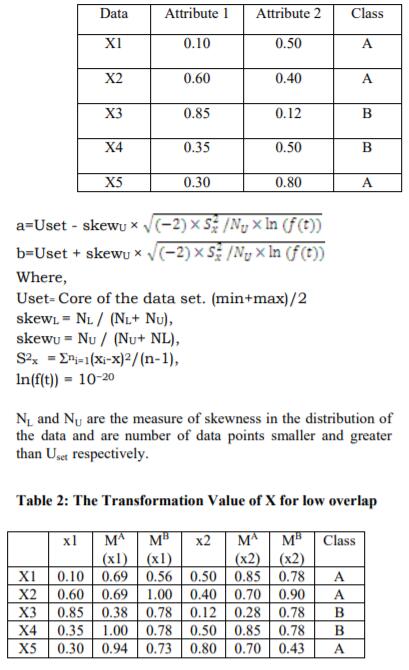
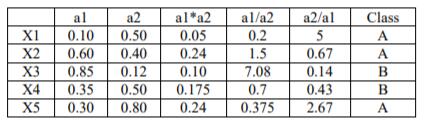
- 建立一个MTD函数
- 计算一个样本两个属性的MTD函数的相交面积
- 若相交面积小，证明两个属性相差够大，可以直接估计。
- 反之，利用样本变量的属性进行运算的合成，变成新的样本属性变量。
这样做的原理其实明显，就是如果相距不够大就模拟数据，相距大就可以用样本进行估计，符合逻辑。除此之外还有其他的人根据这个方法做了改进，基本上是构造这个三角形函数的方式不同，以及估计的假设值不再是简单的运算。如下面这篇文章A non-parametric learning algorithm for small manufacturing data sets，用的是连续输入的x构造一个三角形函数，而不是每个属性值一个函数，也不需要再计算相交面积。而且每个样本x都会有一个tp值，这个值可以理解为这个样本在整体样本中的一个映射，将这个tp值加入模型进行训练，方便模型更加容易找出数据的关系和内部价值。上一节的三角形函数是一个样本数据的关系体现，这里的三角形函数则是整体数据的体现。还有其他几篇文章，也是根据这个方法进行改进的。 